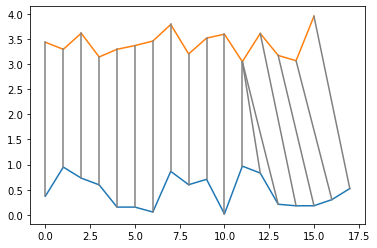
动态时间规整 dynamic time warping (DTW)
1 时间序列距离
设有两段时间序列数据,需测量他们的距离/相似性$ distance(X, Y) $:
$$ \begin{align} X &= x_1,x_2,\cdots,x_{N-1},x_N \\ Y &= y_1,y_2,\cdots,y_{M-1},y_M \end{align} $$
最简单的方法是计算欧式距离:
$$ Dist(X, Y) = \left[ \sum_{i=1}^n |x_i - y_i |^2 \right]^{\frac{1}{2}} $$
但是这要求两段序列长度相等,而且状态变化的速度相等, 因为只有相同时间的数据点之间才会被计算距离。
如不满足上面的要求,可以选择将其中某些数据点的时间(变化速度)扭曲到其他位置对应另一时间序列数据的某些数据点, 这就是DTW算法$^{[1]}$.
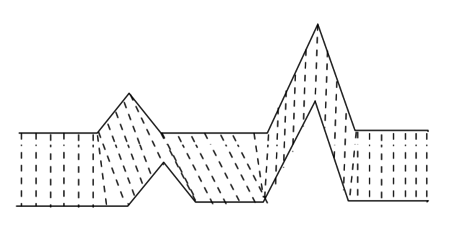
2 DTW
动态时间规整(其实我觉得翻译为扭曲更好)算法,有以下限制$^{[2]}$:
- 两段被测量的时间序列数据各自第一个数据点必须对齐,
- 两段被测量的时间序列数据各自最后一个数据点必须对齐,
- 每个数据点可以和另一段序列的多个点对应测量距离, 反之亦然.
- 数据点测量对齐是单调递增,不可以交叉跨越.例如 $ x_5 <-> y_7 $, 就不能$ x_3 <-> y_7 $, 反之也如此.
测量的是最短距离,可以自由选择两个数据点之间测量函数.
2.1 成本矩阵
定义:
$$ Dist(X_i, Y_j) = Dist(X_i, Y_j) + \min \left[ Dist(X_{i-1}, Y_{j-1}), Dist(X_{i-1}, Y_j), Dist(X_i, Y_{j-1}) \right] \\ \text{where} \quad 1 \leq i \leq N, 1 \leq j \leq M $$
从左到右,从下到上的方式填充成本矩阵,每次都选择累积最小成本(距离/相似性)的值填充到当前"数据点对"对应的成本矩阵位置,于是最终得到两段时间序列数据在动态时间扭曲后的距离(相似性)测量.:
$$ Dist(X, Y) = Dist(X_N, Y_M) $$
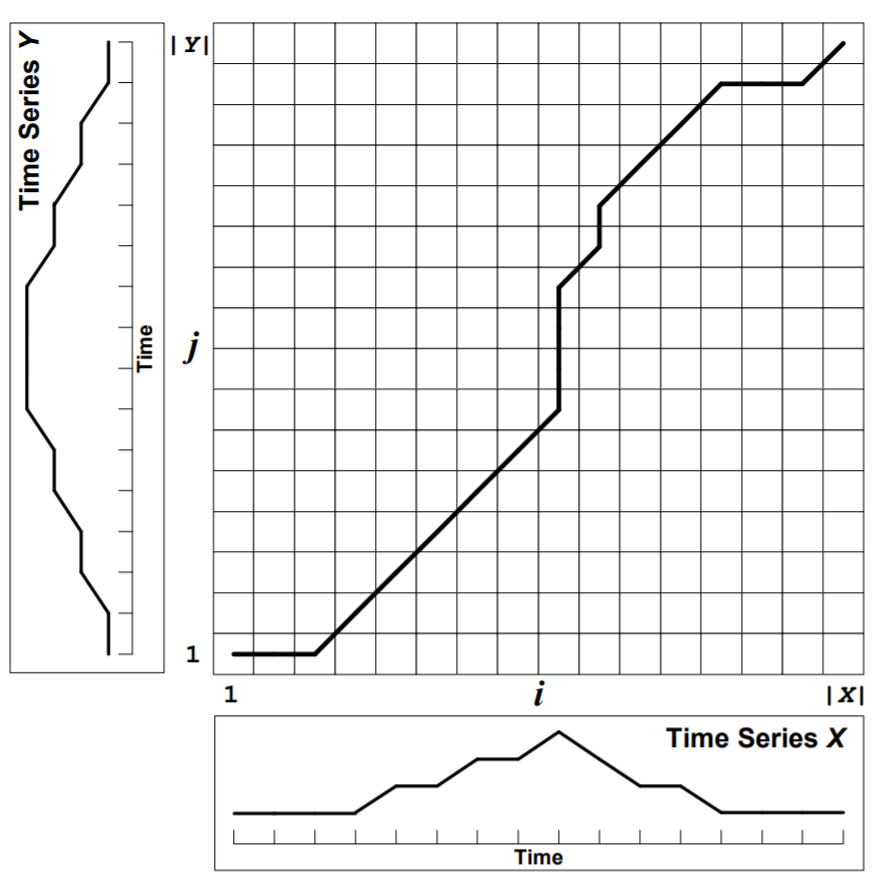
设扭曲时间位置后得到的最小距离路径(观察成本矩阵中的最小距离路径):
$$ W = w_1, w_2, \cdots, w_K \quad \text{where} \max(N,M) \leq K \leq N+M \\ w_k = (i, j), w_{k+1} = (\acute{i}, \acute{j}), i \leq \acute{i} \leq i+1, j \leq \acute{j} \leq j+1 $$
成本矩阵中任意$ D(i, j) $保存的值,其实是从$ D(1, 1) \text{ to } D(i, j) $, 最小距离(最佳相似性)路径的所有沿途对应数据点距离度量求和.
$$ Dist(X,Y) = Dist(W) = \sum_{k=1}^K Dist(w_k) $$
通过计算成本矩阵的相反过程,可以回溯得到最佳距离路径.
$$ \begin{align} W_k &= (i, j) \\ w_{k-1} &= \arg \min Dist(i-1, j), Dist(i, j-1), Dist(i-1, j-1) \end{align} $$
2.2 计算复杂度
成本矩阵的时间和空间计算复杂度都是 $ O(NM) $, 毕竟每个矩阵元素都需要被计算填充,也就是所有点对应的位置都要被计算一次。如果序列很长,可能会造成计算量以及内存占用无法接受, 但如果只需要计算最短时间扭曲距离/相似性,不需要得到最佳距离路径,那么考虑到从左到右计算成本矩阵时并没有用到上一步之前的矩阵数据,因此这里可以每次丢弃之前的矩阵数据,每次保留两行两列. 因此矩阵内存占用可以极大缩小。
三个可选方法可以提高计算性能
- 考虑到绝大多数最短距离路径其实并没有偏离成本矩阵(1,1)->(N,M)对角线太远,也就是说,偏离对角线距离过远的成本矩阵元素其实可以不被计算. 只计算下图阴影区域成本矩阵元素即可(Sakoe-Chuba Band$^{[3]}$, Itakura Parallelogram$^{[4]}$).

- 在对计算精度要求不高时, 也可以先计算低精度路径,得到大致路径后再计算高精度, 可以将成本矩阵缩放到低分辨率计算. 如下图,先对完整的矩阵(直接将待测量时间序列做下采样)采样得到粗糙时间的成本矩阵,计算得到大致路径后,再计算更高精度路径和距离$^{[5][6]}$.
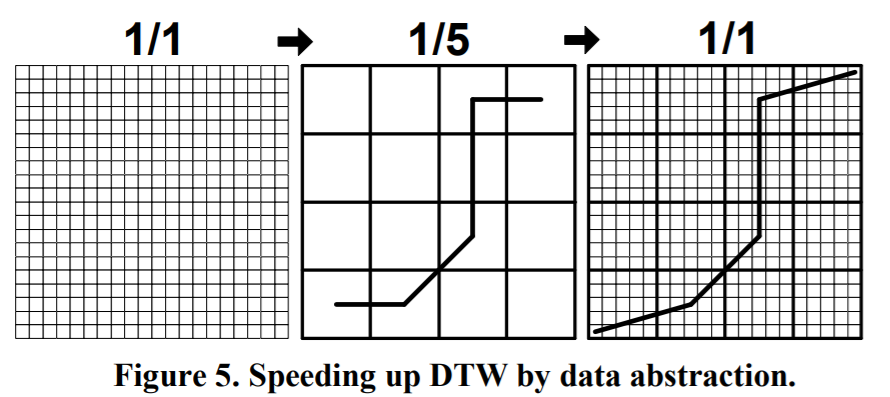
- 在有大量时间序列数据需要测量相似性/距离时,例如要从数千段时间序列中找出和待比较时间序列之间最短距离的其它时间序列,可以先将所有时间序列数据聚类,然后只在相同类别的时间序列之间使用DTW算法,虽然这不能减少单个DTW计算时间,但可减少整个任务计算时间需求.
3 代码实验
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def DTW(X, Y, distance=lambda a, b: np.linalg.norm(a-b)):
""" dynamic time warping """
# cacluate the cost matrix
N, M = len(X), len(Y)
cost = np.ones([N, M]) * np.inf
for i in range(N):
for j in range(M):
# Dist(X_i, Y_j) = Dist(X_i, Y_j) + \min \left[ Dist(X_{i-1}, Y_{j-1}), Dist(X_{i-1}, Y_j), Dist(X_i, Y_{j-1}) \right]
dist_ij = distance(X[i], Y[j])
dist_pr = min(cost[i-1, j] if i-1>=0 else np.inf, cost[i, j-1] if j-1>=0 else np.inf, cost[i-1, j-1] if i-1>=0 and j-1>=0 else np.inf)
cost[i, j] = dist_ij + ( dist_pr if dist_pr < np.inf else 0 )
# traced back cost matrix to get minimum distance path
i, j = N-1, M-1
path = [(i, j)]
while i>0 or j>0:
condidate = []
if i-1>=0: condidate.append( (cost[i-1, j], (i-1, j)) )
if j-1>=0: condidate.append( (cost[i, j-1], (i, j-1)) )
if i-1>=0 and j-1>=0: condidate.append( (cost[i-1, j-1], (i-1, j-1)) )
# w_{k-1} &= \arg \min Dist(i-1, j), Dist(i, j-1), Dist(i-1, j-1)
i, j = min(condidate)[1]
path.append((i,j))
return cost[N-1, M-1], path
g_X = np.random.uniform(size=18)
g_Y = np.random.uniform(size=16) + 3.0
dist, path = DTW(g_X, g_Y)
print( 'Dist(X, Y) = ', dist )
plt.plot(g_X)
plt.plot(g_Y)
for ij in path:
plt.plot([ij[0], ij[1]], [g_X[ij[0]], g_Y[ij[1]]], 'gray')
plt.show()
Dist(X, Y) = 52.18108187595933
ref:
[1] Dynamic time warping From Wikipedia
[2] FastDTW: Toward Accurate Dynamic Time Warping in Linear Time and Space. Stan Salvador & Philip Chan. KDD Workshop on Mining Temporal and Sequential Data, pp. 70-80, 2004.
[3] Itakura, F. Minimum Prediction Residual Principle Applied to Speech Recognition. In IEEE Trans. Acoustics, Speech, and Signal Proc. vol. ASSP-23, pp 52-72, 1975.
[4] Sakoe, H. & S. Chiba. (1978) Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoustics, Speech, and Signal Proc., Vol. ASSP-26.
[5] Chu, S., E. Keogh, D. Hart & Michael Pazzani. Iterative Deepening Dynamic Time Warping for Time Series. In Proc. of the Second SIAM Intl. Conf. on Data Mining. Arlington, Virginia, 2002.
[6] Keogh, E. & M. Pazzani. Scaling up Dynamic Time Warping for Datamining Applications. In Proc. of the Sixth ACM SIGKDD Intl. Conf. on Knowledge Discovery and Data Mining, pp.285-289. Boston, Massachuseetts, 2000